Manual Cell Counting (by microscope)
Since blood cells are counted per unit volume (per liter), it is vital that the volume of blood, in which the cells are counted, corresponds to a known quantity. This makes the Neubauer counting chamber a useful method.
 |
A special objective slide on which two 3 x 3 mm long counting grids were engraved comprises the Neubauer counting chamber. |
Neubauer counting chamber from above with cover slip
Notice the two counting grids which are recognized as crosses. |
| |
|
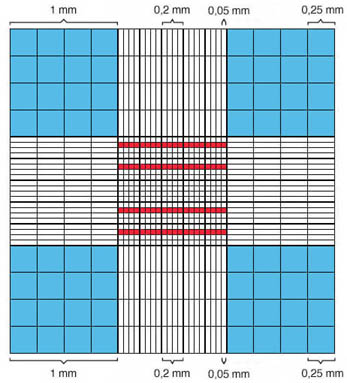 |
The counting grid is composed of 9 big squares, measuring 1 x 1 mm . From these squares, the central square contains 25 medium sized squares each measuring 0.2 x 0.2 mm. These are further divided into 16 small squares each measuring 0.05 x 0.05 mm. The large central square is also called the erythrocyte grid. The squares highlighted in red correspond to 80 small squares, that are used to establish the erythrocyte and platelet counts. The large squares marked in blue are used to establish the leukocyte count. |
Schematic representation of the
Neubauer counting chamber's counting grid:
blue = area of the leukocyte count
red = areas of the erythrocyte and platelet counts |
|
| |
|
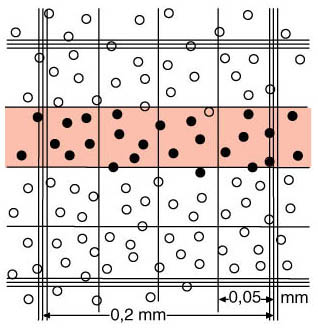 |
During the chamber count, all cells that lie on the left and the lower border or that just touch it are counted. None of the cells on the upper and the right border or those that just touch it will be counted. This procedure is also known as the L-form rule
 Filled circles = count Filled circles = count
 Empty circles = do not count Empty circles = do not count |
Schematic representation of a medium-sized square
(0.2 x 0.2 mm) of the Neubauer counting chamber's erythrocyte grid. |
| |
|
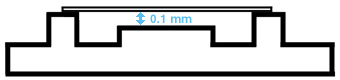
Schematic representation of the Neubauer counting chamber
side view
blue = chamber depth |
On both sides of the counting grid, an edge can be found. A cover slip is placed on top of it. If the cover slip is properly placed, a distance of 0.1 mm (chamber depth) will exist between the counting grid and the cover slip. The volume that is over the squares of the counting net corresponds to 0.1µl in a large square (1mm x 1mm x 0.1 mm = 0.1mm3 = 0.1µl) and to 0.00025µl in a small square (0.05 mm x 0.05 mm x 0.1 mm = 0.00025mm3 = 0.00025µl). |

Photographic representation of the Neubauer counting chamber
side view
Notice the short distance of 0.1 mm between
object slide and the cover slip |
Manual Erythrocyte Counting
In a manual erythrocyte count, 10 µl of EDTA blood (collected with an Eppendorf pipette) is diluted in 1990 µl of isotonic erythrocyte dilution solution. This results in a dilution of 1:200. This suspension must be well-mixed and be immediately placed into the counting chamber. After approximately 3 minutes, the erythrocytes will have settled, and one may begin counting the erythrocytes in 80 small squares.
The calculation of the erythrocyte count is achieved by following the formula below using these factors:
- the number of erythrocytes (Ec) counted in the small squares,
- the dilution of the cell solution,
- the number of counted small squares,
- the volume above one small square, and
- the conversion factor which is necessary in order to arrive at the volume of one liter. Since we are dealing with one µl, this is equal to 106 (1 µl = 1 x 106 L or 1 L = 1 x 106 µl).
number of counted erythrocytes(I) x dilution(II)
number of counted squares(III) x volume above one small square(IV) |
= |
erythrocytes
µl |
= |
erythrocytes x 106(V)
L |
Example with 420 counted erythrocytes:
420 Ec x 200
80 x 0.00025 µl |
= |
84,000 Ec
0.02 µl |
= |
4,200,000 Ec
µl |
= |
4,200,000 Ec x 106
L |
= |
4.2 x 1012 Ec/L |
Minimum number of erythrocytes to be counted = 400
In 80 small squares, around 400 erythrocytes are counted for normal erythrocytes values. This yields a coefficient of variation (variability) of ±5%. This constitutes the highest acceptable amount of random error (accuracy). If, however, the erythrocytes are decreased in one patient (anemia, except for the thalassemias), scattering increases and the accuracy, therefore, decreases. In polycythemia on the other hand, the accuracy increases with an increasing erythrocyte count. In this latter caes, a higher dilution must be used. In low erythrocyte counts on the other hand, the number of counted squares must be increased or the dilution (e.g. 1:100) must be decreased in order to bring the accuracy into an acceptable range.
Manual Leukocyte Counting
IIn the mnual leukocyte count, 50 µl of EDTA-blood (collected with an Eppendorf pipette) is mixed together with 950 µl dilution solution (e.g. Türk's solution, collected with an Eppendorf pipette). This constitutes a dilution of 1:20. The erythrocytes will be lysed, and the leukocyte nucleus will be stained. The counting chamber is immediately filled after mixing. After 2 minutes, one may begin counting the leukocytes in the 4 large squares.
Calculation of the leukocyte count is achieved by following the formula below using these factors:
- the number of leukocytes (Lc) counted in the big squares,
- the dilution of the cell solution,
- the number of counted big squares,
- the volume above a big square, and
- the conversion factor which is necessary in order to come to the volume of one liter. Since we are moving in the µl area, this is equal to 106 (1 µl = 1 x 106 L or 1 L = 1 x 106 µl).
number of counted leukocytes(I) x dilution(II)
number of counted squares(III) x volume above one big square(IV) |
= |
leukocytes
µl |
= |
leukocytes x 106(V)
L |
Example with 150 counted leukocytes:
150 Lc x 20
4 x 0.1 µl |
= |
3,000 Lc
0.4 µl |
= |
7,500 Lc
µl |
= |
7,500 Lc x 106
L |
= |
7.5 x 109 Lc/L |
Minimum number of leukocytes to be counted = 100
Since the leukocyte count already shows greater physiologic variations, a coefficient of variation of ±10% is acceptable. At least 100 leukocytes must be counted to achieve this. As previously mentioned, accuracy decreases with decreasing leukocyte counts and increases with increasing values. In low leukocyte counts, either the number of counted squares must be increased or the dilution decreased (e.g. 1:10) in order to bring the accuracy into the acceptable range.
Since normoblasts are not recognized as such in this procedure, a large number of normoblasts can invalidate results. This is also true for mechanical leukocyte counts. The number of normoblasts can only be accurately identified in a blood film and is expressed as the number of normoblasts per 100 leukocytes. If there are more than 5 normoblasts per 100 leukocytes, a correction must be used.
The normoblast correction is achieved by using the formula below:
number of counted leukocytes x 100
number of normoblasts per 100 leukocytes + 100 |
| Example with 12 normoblasts per 100 leukocytes with a leukocyte count of 5.6 x 109/L: |
5.6 x 109/L x 100
12 + 100 |
= |
5.6 x 109/L x 100
112 |
= |
5.6
1.12 |
x 109/L |
= |
5.0 x 109/L |
Manual Platelet Counting
In a platelet count, 50 µl EDTA blood (collected with an Eppendorf pipette) is mixed in 950 µl dilution solution (collected with an Eppendorf pipette). This results in a dilution of 1:20. The mixture must stand approximately 5 minutes so that the erythrocytes are completely lysed. Then the suspension is mixed and put into the counting chamber. The chamber is left in a moist environment for 20-30 minutes so the platelets can settle without the chamber drying. Like the erythrocyte count, 80 small squares are counted.
Calculation of the platelet count is achieved by using the formula below using these factors:
- the number of platelets (Tc) counted in the small squares,
- the dilution of the cell solution,
- the number of counted squares,
- the volume above a square, and
- the conversion factor which is necessary in order to come to the volume of one liter. Since we are moving in the µl area, this is equal to 106 (1 µl = 1 x 106 L or 1 L = 1 x 106 µl).
number of counted platelets(I) x dilution(II)
number of counted squares(III) x volume above one small square(IV) |
= |
platelets
µl |
= |
platelets x 106(V)
L |
Example with 230 counted platelets:
230 Tc x 200
80 x 0.00025 µl |
= |
4,600 Tc
0.02 µl |
= |
230,000 Tc
µl |
= |
230,000 Tc x 106
L |
= |
230 x 109 Tc/L |
Minimum number of platelets to be counted = 100
A coefficient of variation of ±10% is also acceptable for platelets. At least 100 platelets must be counted. In the case of low platelet counts, the number of counted squares must be increased or the dilution must be decreased (e.g. 1:10) in order to bring the accuracy into an acceptable range. One can also count a second chamber.
Manual leukocyte differential
To manually classify leukocytes, a blood film is stained with May-Gruenwald-Giemsa. The different types of leukocytes from the film are counted under a microscope. Since the leukocytes are not evenly distributed in the film and the same cell may not be counted more than once, the preparation should be systematically screened.
 |
 |
| Pull film |
Push film |
At least 100 leukocytes should be counted and classified. Ideally, 2 x 100 cells (in two blood films) should be counted. It is nearly impossible to count more than 100 leukocytes in severe leukopenias. On the other hand, in the case of very high leukocyte counts, 400 leukocytes should be counted. Percentages achieved in this way are converted to absolute values via the leukocyte count (e.g. 20% lymphocytes with a leukocyte count of 6.0 x 109/L corresponds to an absolute lymphocyte count of 0.2 x 6.0 = 1.2 x 109/L).
Precision must be discussed again. Since leukocytes such as eosinophils and basophils only constitute a small part of the total number of leukocytes, the accuracy of their counts is rather small when only 100 leukocytes are counted. This is especially important when the leukocyte count is very high (e.g. 1 eosinophil per 100 leukocytes in a leukocyte count of 60.0 x 109/L already corresponds to 60.0 x 107/L). To what degree the leukocyte differential values can vary, independent of the number of differentiated cells, can be determined from the Rümke table (see below).
$ If the actual percentage of a patient's basophils are 5%, for example, the value found by counting 100 leukocytes may be between 2 and 11%. Only by counting 10,000 cells (performed accurately only by automated counters), has the obtained value a precision of ±10%. If the percentage of a cell type is 50% a precision of ±10% is achieved with 500 counted leukocytes.$
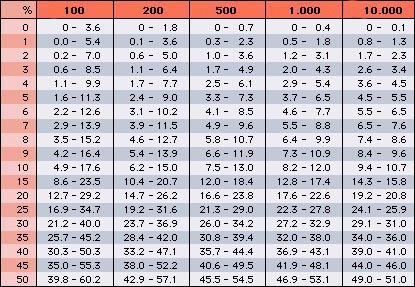 |
Rümke table
% = percentage of a type of leukocyte to the total number
shaded dark red = percentage of identified leukocytes
(Table modified from the CD-ROM "Das interaktive Handbuch der Hämatologie") |
Manual Reticulocyte Counting
Reticulocytes are stained without fixation (supravital staining) with either new methylene blue or brilliant cresyl blue and applied to an ordinary glass slide. A special eyepiece is used which reduces the field of vision to a small square for counting. Around 1000 erythrocytes (500 in each of the two films) are counted, and the reticulocytes which are recognizable due to their reticular markings are counted. The number of reticulocytes per erythrocytes is expressed as a percent.
The lower the number of reticulocytes, the more inaccurate the value. When 1000 erythrocytes are counted, a coefficient of variation of ±10% is achieved for a reticulocyte percentage of 1-2% (= normal range).
Created on 6/3/2000. Last changed on 8/3/2000. Address all remarks to Dr. med. U. Woermann







